Atomare Auflösung für Jedermann?

[Chromatic correction: A revolution in electron microscopy Vortrag von Joachim Zach bei der Royal Society of Microscopy 2009 in London]

Grundlagen

Als das Elektronenmikroskop erfunden wurde, erhoffte man sich im Vergleich zur Lichtmikroskopie eine weitgehende Auflösungsverbesserung, da die Wellenlänge der Elektronen bei einer hinreichend großen Beschleunigungsspannung weit unter der Lichtwellenlänge liegt.

\lambda=\frac{h}{\sqrt{2{m_\omicron}eU}}

Einem von der Spannung U [in Volt] beschleunigtem Elektron kann man gemäß der de-Broglie-Beziehung die Wellenlänge λ zuschreiben [h Plancksches Wirkungsquantum, e Elementarladung, m0 Ruhemasse des Elektrons].

Demnach hat ein mit 10 kV beschleunigtes Elektron eine Wellenlänge von 0.012 nm, seine Geschwindigkeit entspricht etwa 10% der Lichtgeschwindigkeit. Bei noch höheren Beschleunigungsspannungen muss man die relativistische Korrektur berücksichtigen.

\lambda=\frac{h}{\sqrt{2{m_\omicron}eU}}\cdot\frac{1}{\sqrt{1+\frac{eU}{2{m_\omicron}c^2}}}

Bei 200 kV Beschleunigungsspannung erreicht das Elektron 70% der Lichtgeschwindigkeit, es hat eine Wellenlänge von 0.0025 nm.

d=N\cdot\frac{\lambda}{sin\space\alpha}

Die theoretisch mögliche Auflösungsgrenze d ergibt sich aus der Wellenlänge λ und dem halben Öffnungswinkel α des Elektronenbündels (gegeben durch den Blendendurchmesser). N ist etwa eins, der genaue Wert hängt vom gewählten Auflösungskriterium ab.

Für unkorrigierte Mikroskope beträgt der halbe Öffnungswinkel typischerweise 10 mrad, wodurch die theoretische Auflösungsgrenze bei der hundertfachen Elektronenwellenlänge (0.25 nm) liegt. Für ein korrigiertes Mikroskop kann bis zu einem halben Öffnungswinkel von 50 mrad abgebildet werden, das ergäbe eine Auflösungsgrenze von 0.05 nm.

Leider haben Linsen für Elektronenmikroskope sehr schlechte optische Eigenschaften (Linsenfehler), die es nicht erlauben, die theoretische Auflösungsgrenze auch wirklich zu erreichen. Auflösungsbegrenzend wirken hauptsächlich der Farbfehler und der Öffnungsfehler. Bei gegebenen Fehlerkoeffizienten für Öffnungsfehler Cs und Farbfehler Cc ergibt sich die jeweilige Auflösungsgrenze zu (A und B sind Faktoren der Größenordnung eins analog zu N):

Öffnungsfehler

d_s=B\cdot\sqrt[4]{\lambda^3\cdot{C_3}}

Farbfehler

d_c=A\cdot\sqrt{\lambda\cdot\frac{\Delta{E}}{E}\cdot{C_c}}

Demnach beeinflussen folgende Mikroskopeigenschaften die Auflösung:

• die Beschleunigungsspannung U legt λ und über die Beziehung E=e·U auch die Energiebreite ΔE/E fest
• die Brennweite der Objektivlinse f bestimmt die Größe der Fehlerkonstanten
• die Quelle ist maßgeblich für die Energiebreite der Elektronen ΔE/E

Konservative Vorgehensweise

Historisch gesehen versuchte man, die Auflösung trotz der Linsenfehler zu verbessern, indem man genau diese Parameter in Richtung Hochauflösung optimierte. Diese Zielrichtung war der Antrieb für die gesamte Entwicklung der Elektronenmikroskopie in den letzten dreißig Jahren.

Verwendung einer sehr hohen Beschleunigungsspannung

Die Verwendung von sehr hohen Beschleunigungsspannungen führte zu den riesigen Megavoltmikroskopen, die ein eigenes Gebäude brauchen und von denen es weltweit nur eine Hand voll Exemplare gibt.

Einsatz von kurzbrennweitigen (starken) Objektivlinsen:

Zur Reduktion des Öffnungsfehlers steht als einziger freier Parameter der Öffnungsfehlerkoeffizient zur Verfügung. Er ist in etwa durch die Brennweite der Objektivlinse gegeben. Bei Immersion (das heißt, die Probe befindet sich innerhalb des Linsenfeldes) reduziert er sich auf die halbe Brennweite. Durch die räumlichen Gegebenheiten kann diese aber nicht wesentlich unter 1 mm reduziert werden. Aber starke Objektivlinsen haben mehrere Nachteile:

• Sie verkleinern den für die Probenmanipulation vorhandenen Raum.
• Die großen Feldstärken erfordern teures und empfindliches Spezialmaterial, da Sättigungseffekte minimiert werden müssen.
• Man benötigt dicke Spulen mit entsprechend großem Platzbedarf, deren hohe Verlustleistung eine aufwendige Kühlung erfordert.

Erniedrigung der Energiebreite:

Neuartige Elektronenquellen mit niedriger Energiebreite wie Schottky- und Feldemissionsquellen benötigen eine aufwendige Vakuumtechnik (Ultrahochvakuum). Ohne Farbfehler wäre mit diesen Quellen eine atomare Auflösung schon bei 200 kV zu erreichen.

Der Königsweg der Korrektur

Otto Scherzer schlug vor, die Linsenfehler durch die Verwendung nicht-rotationssymmetrischer Bauelemente zu kompensieren. Zunächst wurde versucht, den Öffnungsfehler zu beseitigen. In den 60er Jahren setzte man zu diesem Zweck elektrische/magnetische Quadrupole ein. Als das Darmstadt-Korrektor Projekt (weitere Informationen dazu hier) etwa zehn Jahre lang lief, konnte erstmals nachgewiesen werden, dass man mit einem Quadrupol/Oktupol-Korrektor sowohl den Farb- als auch den Öffnungsfehler prinzipiell kompensieren kann. Die erste Auflösungsverbesserung durch Verwendung von Korrektoren wurde 1995 von Haider und Zach anhand eines Niederspannungs-SEM demonstriert.

Der nächste Meilenstein wurde im Oktober 2008 erreicht, als der erste Farb- und Öffnungsfehlerkorrektor für ein TEM dem Argonne National Laboratory zur Verfügung gestellt werden konnte. Er wurde von CEOS im Rahmen des Team-Projektes entwickelt.

Da nun also Farb- und Öffnungsfehlerkorrektur für SEM und TEM zur Verfügung stehen, könnte man auf die oben aufgeführten selbstauferlegten Einschränkungen verzichten und trotzdem atomare Auflösung für eine aberrationsfreie Abbildung erreichen. Welche Anwendungsmöglichkeiten ergeben sich daraus?

Definition einer aberrationsfreien Abbildung (aberration free imaging-AFI)

Aberrationsfreie Abbildung heißt in unserer Definition, dass die nach der Korrektur der Hauptfehler noch vorhandenen Fehler höherer Ordnung in der Summe keine allzu große Phasenverschiebung der Elektronenwelle verursachen. Wir definieren die maximale Phasenschiebung so, dass die Summe aller Aberrationen einer bestimmten azimutalen Zähligkeit nicht mehr als Π/4 ist und zwar für den gesamten Raumfrequenzbereich, der zum Erreichen der Zielauflösung benötigt wird.

Eine Revolution bahnt sich an

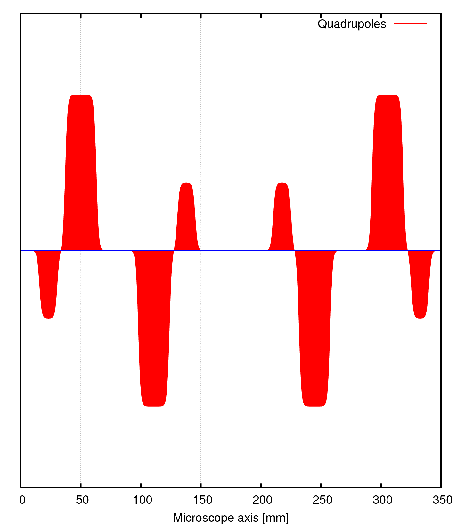
Hier ist schematisch die Anordnung der optischen Elemente im Korrektor dargestellt. Der Aufbau ist spiegel­sym­metrisch, um außeraxiale Aberrationen zu reduzieren. Die Amplituden haben willkürliche Einheiten.
Der Strahlengang wird von Quadrupolen geformt. Selbst bei einer Beschleunigungsspannung von 200 kV kann die magnetische Erregung der Quadrupole unterhalb von 25 Ampere­win­dungen bleiben.

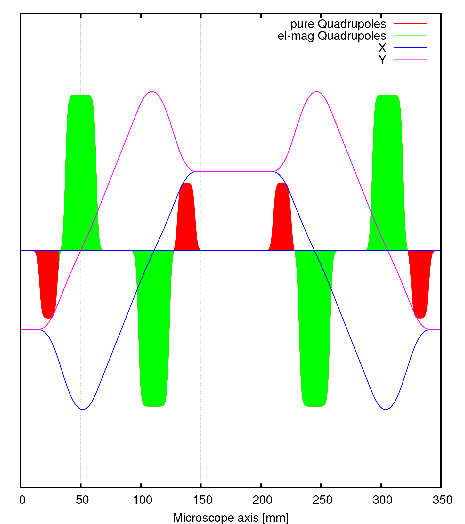
Der Strahlengang zeigt vier astigmatische Zwischenbilder, die in den vier Korrekturstücken liegen (siehe auch Korrekturprinzip weiter unten).

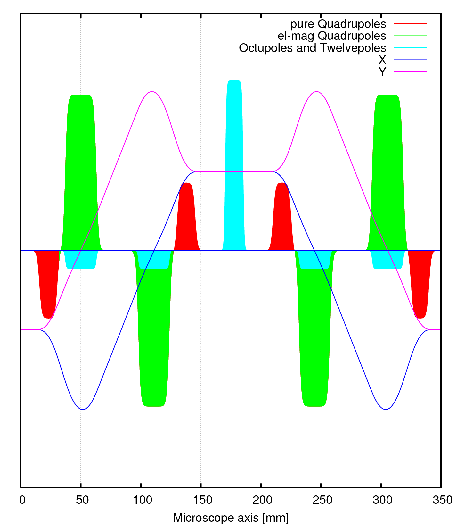
Türkis dargestellt sind die Oktupole und Zwölf­pole in den Korrekturstücken und in einem zentralen Multipol.

Korrekturprinzip

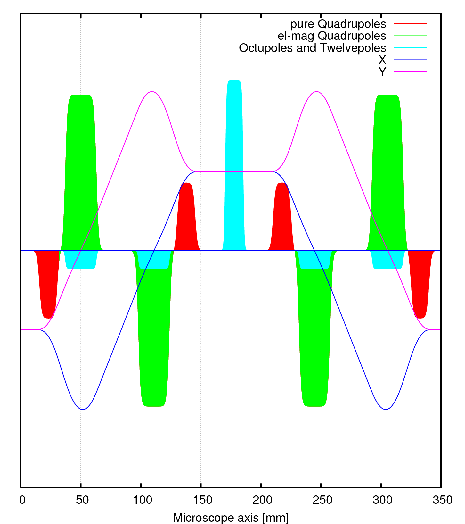
• Farbfehlerkorrektur: elektrisch-magnetische Quadrupole in den Korrekturstücken (Prinzip des Wienfilters erster Ordnung - wie schon 1995 von Zach/Haider).
• Öffnungsfehlerkorrektur: Oktupole und Zwölfpole in den Korrektur­stücken
• Korrektur des vier- und sechszähligen Astigmatismus: Oktupol und Zwölfpol im zentralen Multipol

Durch die unkorrigierten Aberrationen kommt es zu Phasenverschiebungen, deren Summe aber das Kriterium für eine aberrationsfreie Abbildung bei 0.05 nm erfüllt.

Mit einem korrigierten 200 kV Elektronenmikroskop ist atomare Auflösung möglich.

Niederspannungsmikroskopie mit atomarer Auflösung

In korrigierten Mikroskopen braucht man keine hohe Strahlenergie, um atomare Auflösung zu erreichen. Die Frage ist nun, wie stark man die Beschleunigungsspannung bei einer Zielauflösung von 0.1 nm erniedrigen kann.

Um das zu beantworten skalieren wir das System auf 30 kV herunter und diskutieren seine Eigenschaften. Unter Annahme einer LaB6-Quelle berechnen wir die restlichen Phasenverschiebungen, sie bleiben alle bis auf die Sternaberration 7. Ordnung in der gewünschten Größenordnung. Aber selbst diese Phasenschiebung kann halbiert werden, indem man sie zum Beispiel mit dem normalen zweifachen Astigmatismus ausgleicht.

Mit einem korrigierten 30 kV Mikroskop ist die atomare Auflösung von 0.1 nm zu realisieren.

Standard-TEM mit atomarer Auflösung

Lange Zeit wurden "normale" TEMs bei 100 kV und mit einer einfachen LaB6-Quelle betrieben. Unter der Annahme einer Energiebreite von 1 eV haben wir die resultierenden Phasenverschiebungen berechnet. Es ergab sich, dass die anvisierte atomare Auflösung in einem korrigierten Mikroskop ohne Weiteres erreicht werden kann.

Mit einem einfachen und preiswerten Mikroskop kann die Leistung unkorrigierter high-end Geräte erzielt werden.

Einfache Objektivlinsen mit atomarer Auflösung

Noch bis vor einigen Jahren durfte man nur in Transmissionsmikroskopen mit sehr starken Objektivlinsen eine gute Auflösung erwarten. Das bedeutete aber, dass die Probe in die winzige Lücke zwischen den Polschuhen gequetscht werden musste und einem sehr hohen magnetischen Feld ausgesetzt war.

In einem farbfehlerkorrigierten Mikroskop dagegen kann man problemlos eine schwache Objektivlinse verwenden. Wir haben einen Modellkorrektor berechnet, bei dem die gesamte Anordnung von Linse und Korrektor nur 35 cm Platz benötigt. Das ist ein geringerer Platzbedarf als sie eine übliche starke Objektivlinse ohne Korrektor hat.

Allerdings ist im praktischen Fall die Auflösung 0.1 nm schwierig zu erzielen, da man die verschiedenen Aberrationen siebter Ordnung mit anderen Fehlern niedrigerer Ordnung kompensieren müsste. Doch schon für eine Zielauflösung von 0.11 nm bleibt lediglich der Öffnungsfehler 7. Ordnung zum Ausgleichen übrig. Dieser Ausgleich erfolgt in der Praxis nahezu unbemerkt beim Fokussieren.

Der Nachteil einer solchen Anordnung ist allerdings, dass die Stabilitätsanforderungen sehr hoch werden. Dennoch sind sie nicht höher als die im TEAM-Projekt bereits erfüllten. Die große Brennweite erfordert allerdings für hohe Vergrößerungen den Einbau einer zusätzlichen Linse.

Ausblick

Seitdem für Elektronenmikroskope neben der Öffnungsfehlerkorrektur auch eine Farbfehlerkorrektur erhältlich ist, haben Gerätehersteller Freiheitsgrade dazugewonnen. Viele Einschränkungen, die bisher unerlässlich für ein gutes Auflösungsvermögen waren, entfallen. Die heute angebotenen "preiswerten" Geräte zeigen eine Gitterauflösung von bis zu 0.14 nm. Teilweise wird die Auflösung gerade durch den Farbfehler begrenzt, so dass man hier durch den Einbau eines passenden Korrektors zu atomarer Auflösung gelangen kann. Eine relative Stabilität von mindestens 10^-7 wäre schon ausreichend. Deshalb könnte schon bald die "Atomare Auflösung für Jedermann" Wirklichkeit werden.